math Namespace Reference

Classes
class	AdjacencyMatrix
	Матрица смежности для алгоритма Литтла More...
class	CircleObstacle
	Круговое препятствие More...
class	DijkstrasAlgorithm
	Реализация алгоритма Дейкстры More...
struct	Edge
	Ребро между двумя контрольными точками More...
struct	LinearFunction
	Прямая вида ax+by+c=0. More...
struct	Minimums
	Структура для хранения двух минимумов строки/столбца More...
class	OptimalWayCalculator
	Функтор, находящий кратчайший путь между точками More...
struct	PathWayGraph
	Граф вершин между контрольными точками More...
struct	PathWayNode
	Вершина графа More...
struct	Point
	Точка с геометрическими связями More...
class	PolygonObstacle
	Многоугольное препятствие More...
class	TrajectoryCalculator
class	TravellingSalesmansProblem
	Решение задачи коммивояжера More...
struct	TSPNode
	Вершина дерева с соответствующей матрицей смежности More...

Functions
bool	AreThereIntersections (const CircleObstacle &cr_obst, const LinearFunction &line)
	Проверяет, пересекает ли прямая многоугольник
bool	AreThereIntersections (const CircleObstacle &cr_obst, const Point &pnt1, const Point &pnt2)
	Проверяет, пересекает ли отрезок, проведенный через две точки, окружность
bool	AreThereIntersections (const PolygonObstacle &poly_obst, const LinearFunction &line)
	Проверяет, пересекает ли прямая многоугольник
bool	AreThereIntersections (const PolygonObstacle &poly_obst, const Point &pnt1, const Point &pnt2)
	Проверяет, пересекает ли отрезок, проведенный через две точки, многоугольник
double	DistanceBetweenPointsOnCircle (const CircleObstacle &circle, const Point &p1, const Point &p2)
double	DistanceBetweenPointsOnPolygon (const PolygonObstacle &polygon, const Point &p1, const Point &p2)
bool	IsPointInsideCircle (const Point &point, const CircleObstacle &circle)
	Проверяет, находится ли точка внутри окружности
std::pair< Point, Point >	TangentPoints (const CircleObstacle &cr_obst, const Point &point)
	Находит точки касания круга c касательной, проведенной из контрольной точки
std::pair< Point, Point >	TangentPoints (const LinearFunction &tangent, const CircleObstacle &circle1, const CircleObstacle &circle2)
	Находит точки касания кругов с их общей касательной
std::pair< Point, Point >	TangentPoints (const LinearFunction &tangent, const PolygonObstacle &polygon, const CircleObstacle &circle)
	Находит точки касания многоугольника и круга с их общей касательной
std::pair< Point, Point >	TangentPoints (const LinearFunction &tangent, const PolygonObstacle &polygon1, const PolygonObstacle &polygon2)
	Находит точки касания двух многоугольников с их общей касательной
std::pair< Point, Point >	TangentPoints (const PolygonObstacle &poly_obst, const Point &point)
	Находит точки касания многоугольника c касательной, проведенной из контрольной точки
std::vector< LinearFunction >	TangentsBetween (const CircleObstacle &circle1, const CircleObstacle &circle2)
	Находит уравнения общих касательных двух кругов
template<typename T >
std::vector< LinearFunction >	TangentsBetween (const PolygonObstacle &polygon, const T &obstacle)
	Находит уравнения общих касательных многоугольника и другого препятствия
template std::vector< LinearFunction >	TangentsBetween< CircleObstacle > (const PolygonObstacle &polygon, const CircleObstacle &obstacle)
template std::vector< LinearFunction >	TangentsBetween< PolygonObstacle > (const PolygonObstacle &polygon, const PolygonObstacle &obstacle)

Function Documentation

AreThereIntersections() [1/4]

bool math::AreThereIntersections	(	const CircleObstacle &	cr_obst,
		const LinearFunction &	line )

Проверяет, пересекает ли прямая многоугольник

Parameters

cr_obst	круг
line	прямая

Returns

bool: результат проверки

                                                       {
  Point center = cr_obst.GetCenter();
  double radius = cr_obst.GetRadius();
  double dist =
      std::abs(line.a_coef * center.x + line.b_coef * center.y + line.c_coef) /
      sqrt(pow(line.a_coef, 2) + pow(line.b_coef, 2));
  return dist < radius - precision;
}

Here is the call graph for this function:

AreThereIntersections() [2/4]

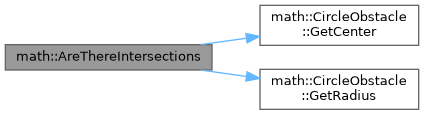
bool math::AreThereIntersections	(	const CircleObstacle &	cr_obst,
		const Point &	pnt1,
		const Point &	pnt2 )

Проверяет, пересекает ли отрезок, проведенный через две точки, окружность

Parameters

cr_obst	круг
pnt1	точка 1
pnt2	точка 2

Returns

bool: результат проверки

                                                {
  double distance = 0;
  Point center = cr_obst.GetCenter();
  double radius = cr_obst.GetRadius();
  Point vector_p1_c = center - point1;
  Point vector_p2_c = center - point2;
  Point vector_p1_p2 = point2 - point1;
  auto module = [](Point p) {
    return lib::DistanceBetweenPoints(p, Point(0, 0));
  };
  auto scalar = [](Point p1, Point p2) { return p1.x * p2.x + p1.y * p2.y; };
  auto vect = [](Point p1, Point p2) {
    return std::abs(p1.x * p2.y - p1.y * p2.x);
  };
 
  if (scalar(vector_p1_p2, vector_p2_c) >= precision) {
    distance = module(vector_p2_c);
  } else if (scalar(vector_p1_p2, vector_p1_c) <= -precision) {
    distance = module(vector_p1_c);
  } else {
    distance = vect(vector_p1_p2, vector_p1_c) / module(vector_p1_p2);
  }
  if (distance - radius <= -precision) return true;
  return false;
}

Here is the call graph for this function:

Here is the caller graph for this function:

AreThereIntersections() [3/4]

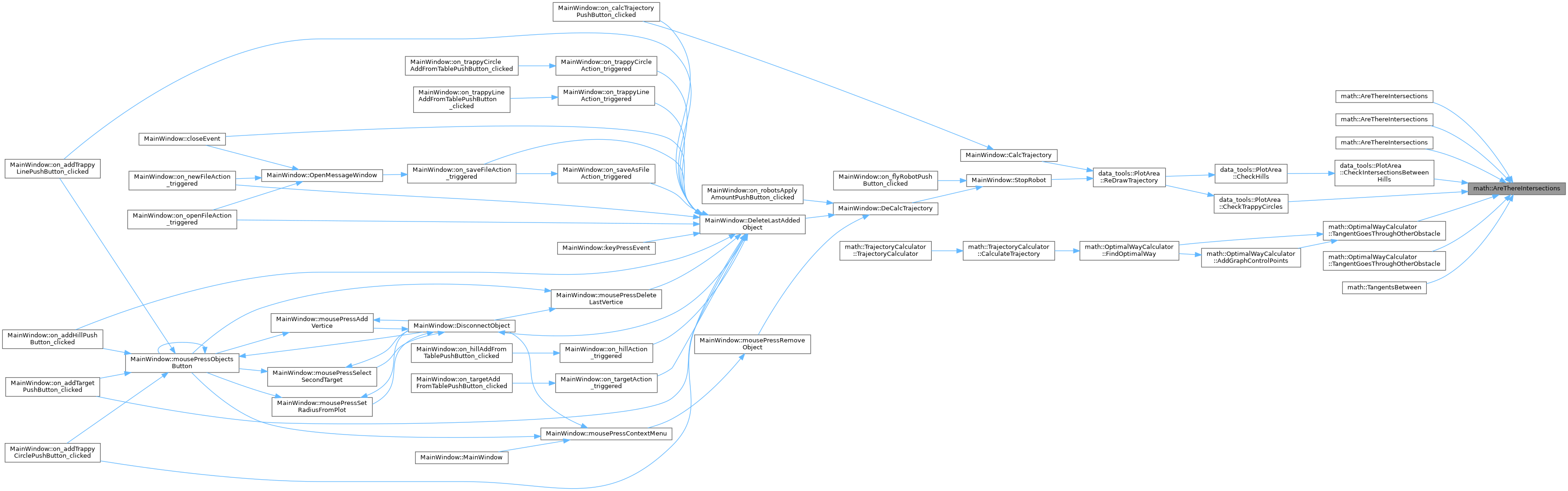
bool math::AreThereIntersections	(	const PolygonObstacle &	poly_obst,
		const LinearFunction &	line )

Проверяет, пересекает ли прямая многоугольник

Parameters

poly_obst	многоугольник
line	прямая

Returns

bool: результат проверки

                                                       {
  std::vector<Point> vertexes = poly_obst.GetVertexes();
  for (std::size_t i = 0; i < vertexes.size(); ++i)
    if ((line.Substitute(vertexes[i]) *
             line.Substitute(vertexes[(i + 1) % vertexes.size()]) <
         -precision))
      return true;
 
  std::size_t prev = ULLONG_MAX;
  for (std::size_t i = 0; i < vertexes.size(); ++i)
    if (std::abs(line.Substitute(vertexes[i])) <= precision) {
      if ((prev + 1 == 0) || (i - prev == 1) ||
          (i - prev == vertexes.size() - 1))
        prev = i;
      else
        return true;
    }
  return false;
}

Here is the call graph for this function:

AreThereIntersections() [4/4]

bool math::AreThereIntersections	(	const PolygonObstacle &	poly_obst,
		const Point &	pnt1,
		const Point &	pnt2 )

Проверяет, пересекает ли отрезок, проведенный через две точки, многоугольник

Parameters

poly_obst	многоугольник
pnt1	точка 1
pnt2	точка 2

Returns

bool: результат проверки

                                              {
  LinearFunction line(pnt1, pnt2);
  std::vector<Point> vertexes = poly_obst.GetVertexes();
  for (std::size_t i = 0; i < vertexes.size(); ++i) {
    LinearFunction v_line(vertexes[i], vertexes[(i + 1) % vertexes.size()]);
    if ((line.Substitute(vertexes[i]) *
             line.Substitute(vertexes[(i + 1) % vertexes.size()]) <
         -precision) &&
        (v_line.Substitute(pnt1) * v_line.Substitute(pnt2) < -precision))
      return true;
  }
  std::size_t prev = ULLONG_MAX;
  for (std::size_t i = 0; i < vertexes.size(); ++i)
    if (std::abs(line.Substitute(vertexes[i])) <= precision) {
      if ((prev + 1 == 0) || (i - prev == 1) ||
          (i - prev == vertexes.size() - 1))
        prev = i;
      else
        return true;
    }
  return false;
}

Here is the call graph for this function:

DistanceBetweenPointsOnCircle()

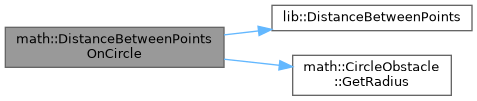
double math::DistanceBetweenPointsOnCircle	(	const CircleObstacle &	circle,
		const Point &	p1,
		const Point &	p2 )

                                                                       {
  if (p1 == p2) return 0;
  double line = lib::DistanceBetweenPoints(p1, p2);
  double cos_alpha = (2 * pow(circle.GetRadius(), 2) - pow(line, 2)) /
                     (2 * pow(circle.GetRadius(), 2));
  return std::abs(cos_alpha) < 1 ? circle.GetRadius() * acos(cos_alpha)
                                 : circle.GetRadius() * M_PI;
}

Here is the call graph for this function:

Here is the caller graph for this function:

DistanceBetweenPointsOnPolygon()

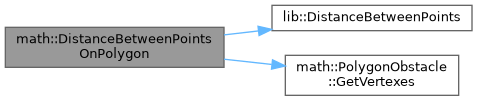
double math::DistanceBetweenPointsOnPolygon	(	const PolygonObstacle &	polygon,
		const Point &	p1,
		const Point &	p2 )

                                                                        {
  std::vector<Point> vertexes = polygon.GetVertexes();
  std::size_t index1 = std::distance(
      vertexes.begin(), std::find(vertexes.begin(), vertexes.end(), p1));
  std::size_t index2 = std::distance(
      vertexes.begin(), std::find(vertexes.begin(), vertexes.end(), p2));
  std::size_t iter = index1;
  double d1 = 0;
  while (iter != index2) {
    d1 += lib::DistanceBetweenPoints(vertexes[iter],
                                     vertexes[(iter + 1) % vertexes.size()]);
    iter = (iter + 1) % vertexes.size();
  }
 
  double d2 = 0;
  while (iter != index1) {
    d2 += lib::DistanceBetweenPoints(vertexes[iter],
                                     vertexes[(iter + 1) % vertexes.size()]);
    iter = (iter + 1) % vertexes.size();
  }
  return std::min(d1, d2);
}

Here is the call graph for this function:

IsPointInsideCircle()

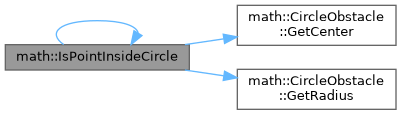
bool math::IsPointInsideCircle	(	const Point &	point,
		const CircleObstacle &	circle )

Проверяет, находится ли точка внутри окружности

Parameters

point	точка
circle	окружность

Returns

bool: результат проверки

                                                                           {
  return (DistanceBetweenPoints(circle.GetCenter(), point) -
          circle.GetRadius()) < 0;
}

Here is the call graph for this function:

Here is the caller graph for this function:

TangentPoints() [1/5]

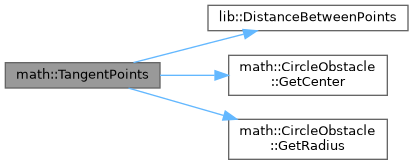
std::pair< Point, Point > math::TangentPoints	(	const CircleObstacle &	cr_obst,
		const Point &	point )

Находит точки касания круга c касательной, проведенной из контрольной точки

Parameters

cr_obst	круг
point	контрольная точка

Returns

std::pair<Point, Point>: точки касательной

                                                          {
  Point center = cr_obst.GetCenter();
  double radius = cr_obst.GetRadius();
  double dist = lib::DistanceBetweenPoints(center, point);
  // Угол между касательной и отрезком, соединяющим точку и центр круга
  double theta = acos(radius / dist);
  double delta = atan2(point.y - center.y, point.x - center.x);
  double delta1 = delta + theta;
  double delta2 = delta - theta;
  double x1_tang_pnt = center.x + radius * cos(delta1);
  double x2_tang_pnt = center.x + radius * cos(delta2);
  double y1_tang_pnt = center.y + radius * sin(delta1);
  double y2_tang_pnt = center.y + radius * sin(delta2);
  return std::make_pair(Point(x1_tang_pnt, y1_tang_pnt),
                        Point(x2_tang_pnt, y2_tang_pnt));
}

Here is the call graph for this function:

TangentPoints() [2/5]

std::pair< Point, Point > math::TangentPoints	(	const LinearFunction &	tangent,
		const CircleObstacle &	circle1,
		const CircleObstacle &	circle2 )

Находит точки касания кругов с их общей касательной

Parameters

tangent	касательная
circle1	круг 1
circle2	круг 2

Returns

std::pair<Point, Point>: точки касательной

                                                                     {
  double a = tangent.a_coef;
  double b = tangent.b_coef;
  double c = tangent.c_coef;
  double x_0 = circle1.GetCenter().x;
  double y_0 = circle1.GetCenter().y;
  double x_1 = circle2.GetCenter().x;
  double y_1 = circle2.GetCenter().y;
  double point1_x =
      (x_0 * pow(b, 2) - (a * (c + y_0 * b))) / (pow(a, 2) + pow(b, 2));
  double point2_x =
      (x_1 * pow(b, 2) - (a * (c + y_1 * b))) / (pow(a, 2) + pow(b, 2));
  double point1_y, point2_y;
  if (std::abs(b) > precision) {
    point1_y = a / b * (-point1_x) - c / b;
    point2_y = a / b * (-point2_x) - c / b;
  } else {
    point1_y = y_0;
    point2_y = y_1;
  }
  Point point1(point1_x, point1_y);
  Point point2(point2_x, point2_y);
  return std::make_pair(point1, point2);
}

Here is the call graph for this function:

Here is the caller graph for this function:

TangentPoints() [3/5]

std::pair< Point, Point > math::TangentPoints	(	const LinearFunction &	tangent,
		const PolygonObstacle &	polygon,
		const CircleObstacle &	circle )

Находит точки касания многоугольника и круга с их общей касательной

Parameters

tangent	касательная
polygon	многоугольник
circle	круг

Returns

std::pair<Point, Point>: точки касательной

                                                                    {
  std::pair<Point, Point> tang_pnts;
  std::vector<Point> vertexes = polygon.GetVertexes();
  for (auto& vertex : vertexes)
    if (std::abs(tangent.a_coef * vertex.x + tangent.b_coef * vertex.y +
                 tangent.c_coef) <= precision)
      tang_pnts.first = vertex;
 
  std::pair<Point, Point> cr_points = TangentPoints(circle, tang_pnts.first);
  for (auto& point : {cr_points.first, cr_points.second})
    if (std::abs(tangent.a_coef * point.x + tangent.b_coef * point.y +
                 tangent.c_coef) <= precision)
      tang_pnts.second = point;
  return tang_pnts;
}

Here is the call graph for this function:

TangentPoints() [4/5]

std::pair< Point, Point > math::TangentPoints	(	const LinearFunction &	tangent,
		const PolygonObstacle &	polygon1,
		const PolygonObstacle &	polygon2 )

Находит точки касания двух многоугольников с их общей касательной

Parameters

tangent	касательная
polygon1	многоугольник 1
polygon2	многоугольник 2

Returns

std::pair<Point, Point>: точки касательной

                                                                       {
  std::pair<Point, Point> tang_pnts;
  std::vector<Point> vertexes1 = polygon1.GetVertexes();
  for (auto& vertex : vertexes1)
    if (std::abs(tangent.a_coef * vertex.x + tangent.b_coef * vertex.y +
                 tangent.c_coef) <= precision)
      tang_pnts.first = vertex;
 
  std::vector<Point> vertexes2 = polygon2.GetVertexes();
  for (auto& vertex : vertexes2)
    if (std::abs(tangent.a_coef * vertex.x + tangent.b_coef * vertex.y +
                 tangent.c_coef) <= precision)
      tang_pnts.second = vertex;
  return tang_pnts;
}

Here is the call graph for this function:

TangentPoints() [5/5]

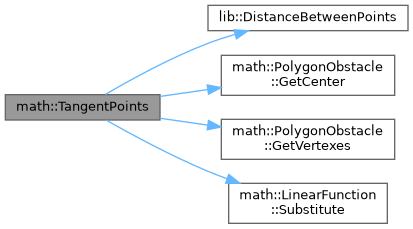
std::pair< Point, Point > math::TangentPoints	(	const PolygonObstacle &	poly_obst,
		const Point &	point )

Находит точки касания многоугольника c касательной, проведенной из контрольной точки

Parameters

poly_obst	многоугольник
point	контрольная точка

Returns

std::pair<Point, Point>: точки касательной

                                                          {
  Point center = poly_obst.GetCenter();
  std::vector<Point> vertexes = poly_obst.GetVertexes();
  Point tang_pnt_1 = vertexes[0];
  double cos_alpha_1 = 1;
  Point tang_pnt_2;
  double cos_alpha_2 = 1;
  double dist_to_cnt = lib::DistanceBetweenPoints(center, point);
  LinearFunction line(center, point);
  for (const auto& vertex : vertexes)
    if (line.Substitute(vertex) * line.Substitute(vertexes[0]) < 0) {
      tang_pnt_2 = vertex;
      break;
    }
  for (const auto& vertex : vertexes) {
    double dist_to_vrtx = lib::DistanceBetweenPoints(vertex, point);
    double dist_cnt_vrtx = lib::DistanceBetweenPoints(center, vertex);
    double new_cos_alpha =
        (pow(dist_to_vrtx, 2) + pow(dist_to_cnt, 2) - pow(dist_cnt_vrtx, 2)) /
        (2 * dist_to_vrtx * dist_to_cnt);
    if ((line.Substitute(vertex) * line.Substitute(tang_pnt_1) > 0) &&
        (new_cos_alpha < cos_alpha_1)) {
      tang_pnt_1 = vertex;
      cos_alpha_1 = new_cos_alpha;
    } else if ((line.Substitute(vertex) * line.Substitute(tang_pnt_2) > 0) &&
               (new_cos_alpha < cos_alpha_2)) {
      tang_pnt_2 = vertex;
      cos_alpha_2 = new_cos_alpha;
    }
  }
  return std::make_pair(tang_pnt_1, tang_pnt_2);
}

Here is the call graph for this function:

TangentsBetween() [1/2]

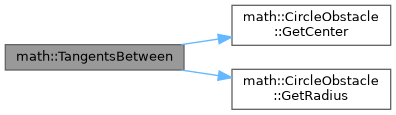
std::vector< LinearFunction > math::TangentsBetween	(	const CircleObstacle &	circle1,
		const CircleObstacle &	circle2 )

Находит уравнения общих касательных двух кругов

Parameters

circle1	круг 1
circle2	круг 2

Returns

std::vector<LinearFunction>: уравнения касательных

                                                                           {
  std::vector<LinearFunction> tangents;
  double x_1 = circle2.GetCenter().x;
  double y_1 = circle2.GetCenter().y;
  double r_1 = circle2.GetRadius();
  double x_0 = circle1.GetCenter().x;
  double y_0 = circle1.GetCenter().y;
  double r_0 = circle1.GetRadius();
 
  auto FindTangent = [&x_1, &x_0, &y_1, &y_0](double r_0, double r_1) {
    double a, b, c;
    if (std::abs(x_1 - x_0) > precision) {
      double root = pow(x_1 - x_0, 2) *
                    (pow(x_1 - x_0, 2) + pow(y_1 - y_0, 2) - pow(r_1 - r_0, 2));
      if (std::abs(root) < precision)
        root = 0;
      else
        root = sqrt(root);
      b = ((r_1 - r_0) * (y_1 - y_0) + root) /
          (pow(x_1 - x_0, 2) + pow(y_1 - y_0, 2));
 
      a = ((r_1 - r_0) - b * (y_1 - y_0)) / (x_1 - x_0);
 
      c = r_0 - a * x_0 - b * y_0;
    } else {
      a = std::abs(y_1 - y_0) / sqrt(pow(r_1 - r_0, 2) + pow(y_1 - y_0, 2));
      b = (r_1 - r_0) / sqrt(pow(r_1 - r_0, 2) + pow(y_1 - y_0, 2));
      c = r_0 - a * x_0 - b * y_0;
    }
 
    return LinearFunction(a, b, c);
  };
 
  for (auto n1 : {-1, 1})
    for (auto n2 : {-1, 1}) {
      bool is_unique = !(std::isnan(FindTangent(r_0 * n1, r_1 * n2).a_coef));
      for (std::size_t i = 0; i < tangents.size(); ++i)
        if (tangents[i] == FindTangent(r_0 * n1, r_1 * n2)) is_unique = false;
      if (is_unique) tangents.push_back(FindTangent(r_0 * n1, r_1 * n2));
    }
  return tangents;
}

Here is the call graph for this function:

Here is the caller graph for this function:

TangentsBetween() [2/2]

template<typename T >

std::vector< LinearFunction > math::TangentsBetween	(	const PolygonObstacle &	polygon,
		const T &	obstacle )

Находит уравнения общих касательных многоугольника и другого препятствия

Parameters

polygon	многоугольник
obstacle	препятствие

Returns

уравнения касательных

                                                               {
  std::vector<LinearFunction> tangents;
  std::vector<Point> vertexes = polygon.GetVertexes();
  for (auto& vertex : vertexes) {
    std::pair<Point, Point> tang_pnts = TangentPoints(obstacle, vertex);
    for (auto& tang_pnt : {tang_pnts.first, tang_pnts.second})
      if (vertex != tang_pnt) {
        LinearFunction line(vertex, tang_pnt);
        if ((!AreThereIntersections(polygon, line)) &&
            (!AreThereIntersections(obstacle, line))) {
          bool is_unique = !std::isnan(line.a_coef);
          for (std::size_t i = 0; i < tangents.size(); ++i)
            if (tangents[i] == line) is_unique = false;
          if (is_unique) tangents.push_back(line);
        }
      }
  }
  return tangents;
}

Here is the call graph for this function:

TangentsBetween< CircleObstacle >()

template std::vector< LinearFunction > math::TangentsBetween< CircleObstacle >	(	const PolygonObstacle &	polygon,
		const CircleObstacle &	obstacle )

TangentsBetween< PolygonObstacle >()

template std::vector< LinearFunction > math::TangentsBetween< PolygonObstacle >	(	const PolygonObstacle &	polygon,
		const PolygonObstacle &	obstacle )